Data Science for Business Applications

Class 13 - Basic Causal Inference

Causal Conclusion

If we run a regression predicting \(Y\) from \(X\) and find that \(X\) is a significant predictor of \(Y\), we would like to conclude that \(X\) causes \(Y\). But it might be the case that:

  • \(Y\) actually causes \(X\).

  • \(X\) and \(Y\) are not actually related in the population; they happen to be correlated in the sample just by chance.

  • A common variable \(Z\) (a confounder) causes both \(X\) and \(Y\).

  • A common variable \(W\) (a collider) is caused by both \(X\) and \(Y\).

Confounders and Colliders

  • A confounder is a third variable that causes both \(X\) and \(Y\) and explains the observed correlation between X and Y.

  • A collider is a third variable that is caused by both \(X\) and \(Y\).

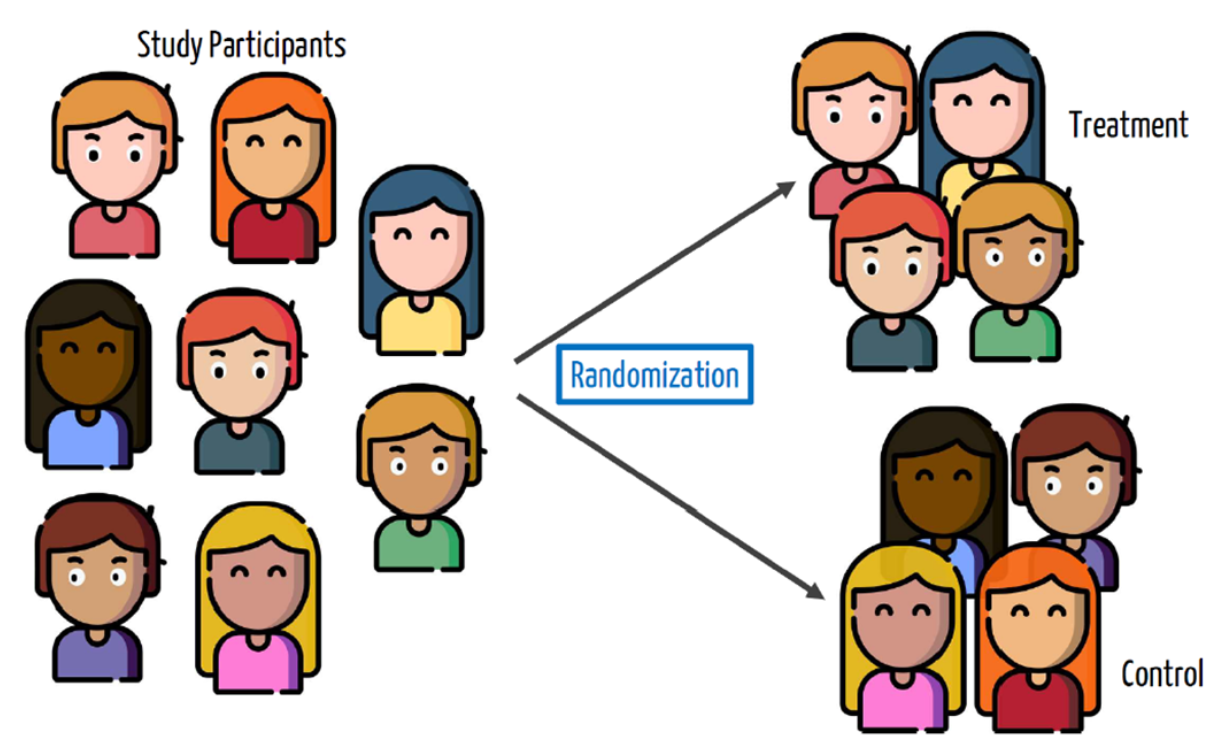
Randomization

One way to make sure the causal conclusion holds is to do it by design:

  • Randomize the assignment of the treatment \(Z\)

  • i.e. Some units will randomly be chosen to be in the treatment group and others to be in the control group.

  • What does randomization buy us?

  • Control for unforeseen factors (confounders)

Confounders

  • Confounder is a variable that affects both the treatment and the outcome

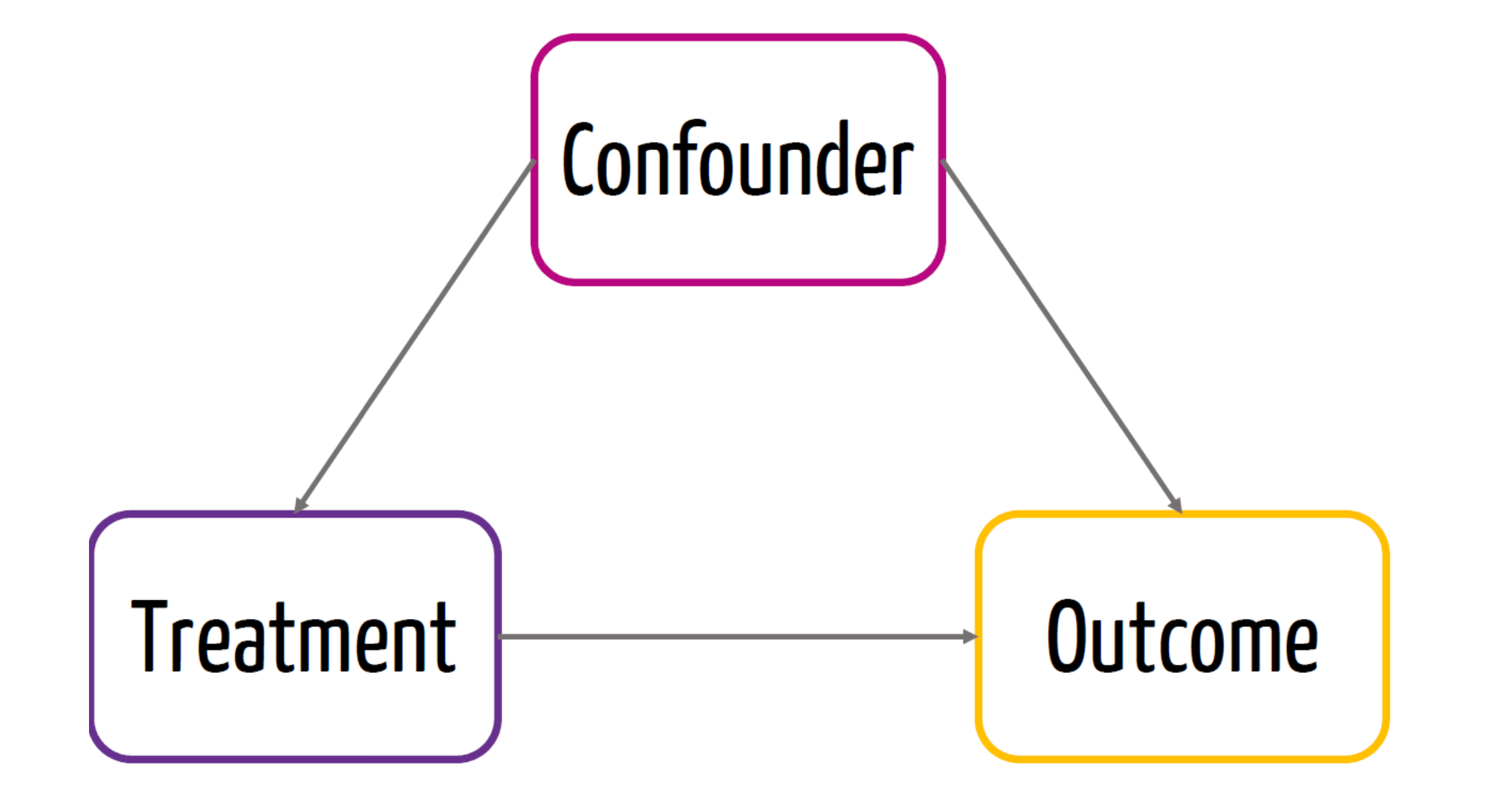
Randomization

  • Due to randomization, we know that the treatment is not affected by a confounder
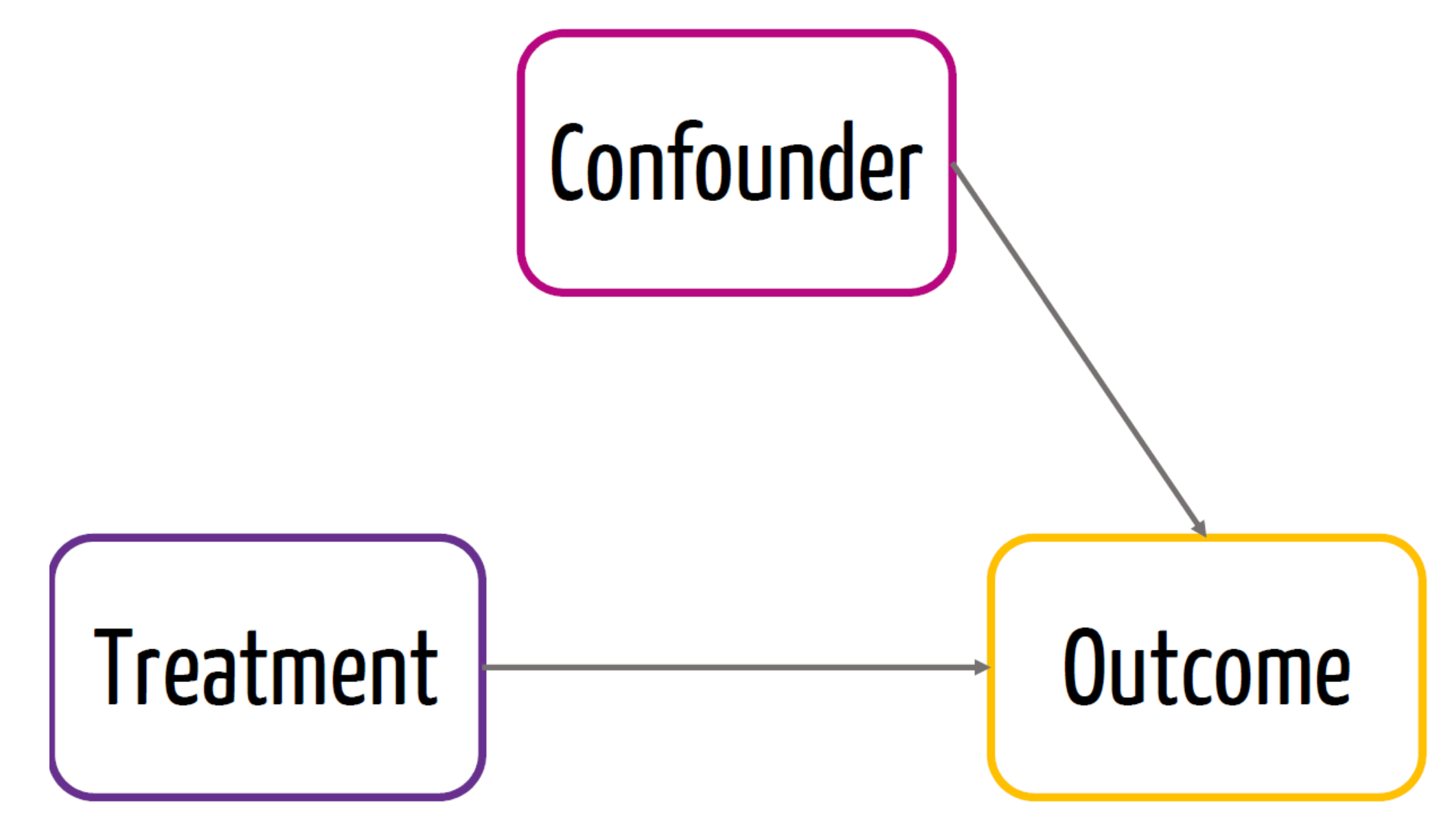
  • This would be the causal effect of the treatment

Randomized controlled trials (RCTs)

  • Often called the gold standard for establishing causality.

  • Randomly assign the \(X\), treatment, to participants

  • Now, any observed relationship between \(X\) and \(Y\) must be due to \(X\), since the only reason an individual had a particular value of \(X\) was the random assignment.

Randomized controlled trials (RCTs)

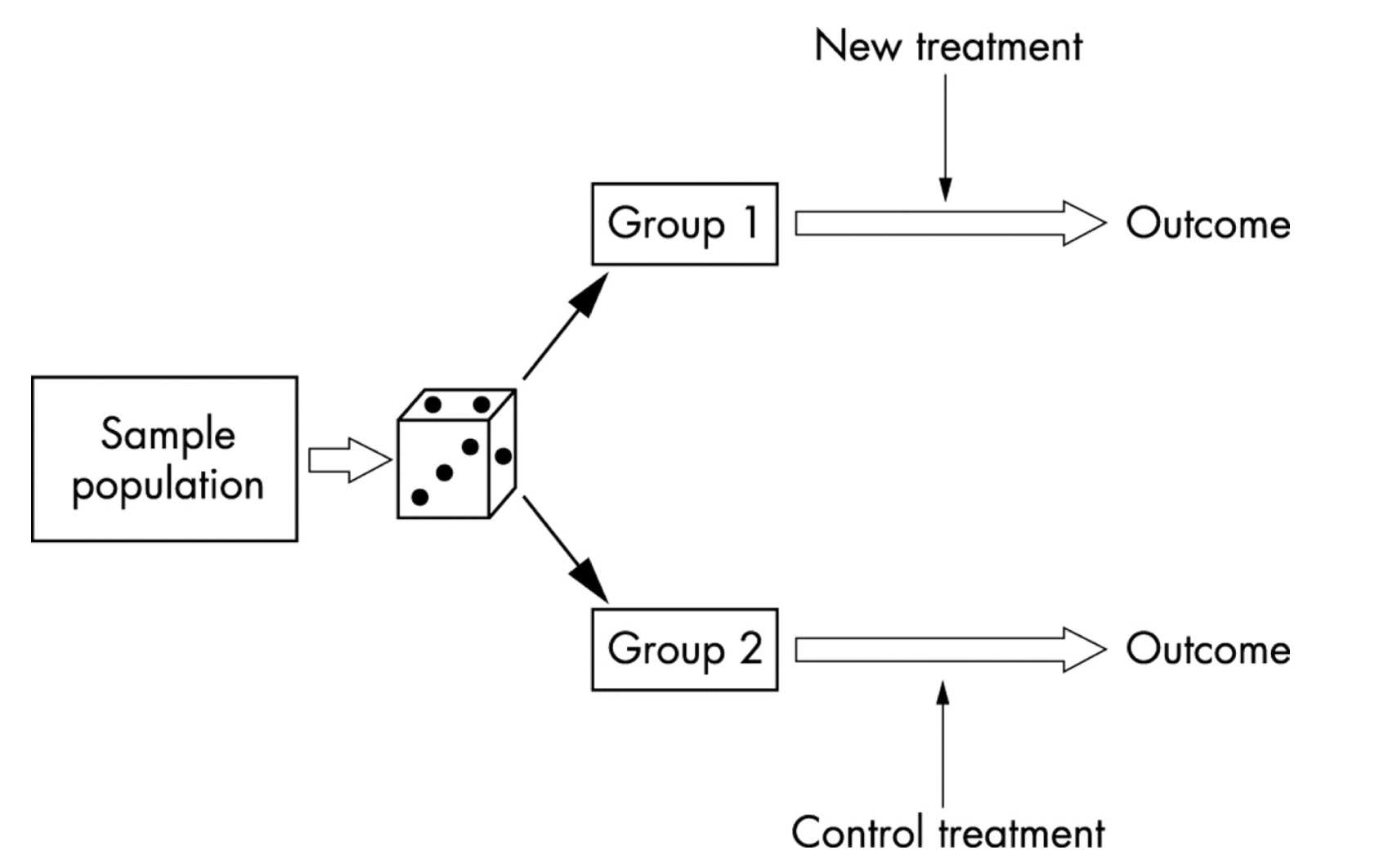
RCT - Steps

  1. Randomize

  2. Check for balance - (balance between the treated and untreated)

  3. Calculate difference in sample means between treatment and control group

Problem with causal inference

  • Suppose you have a headache, and you take an asprin. Then you don’t have a headache. Did the asprin work?
Person Took aspirin Didn’t take aspirin
1 no headache ?
2 no headache ?
3 no headache ?
4 no headache ?
5 ? no headache
6 ? headache
7 ? headache
8 ? headache
  • For any given person, we can only observe one outcome or the other, depending on whether the person took an asprin or not:

Problem with causal inference

  • The best we can do is compute an average treatment effect (ATE): the difference in the proportion of the treatment vs control group \[ \begin{aligned} \text{ATE} &= (\% \text{ headache among aspirin–takers}) \\ &\;\;-\; (\% \text{ headache among non–aspirin–takers}) \\ &= \frac{0}{4} - \frac{3}{4} \\ &= -0.75 \end{aligned} \]

  • Headaches decreased in 75% among those who took aspirin compared to those who didn’t take aspirin.

  • We can only make this conclusion if the treatment was randomly assigned.

Example 1: Vaccine Trial

  • Phase 3 Clinical Trial for the Moderna COVID-19 vaccine

  • \(X\) = got the vaccine, \(Y\) = got COVID-19

  • Randomly assign study participants to get either the vaccine (an treatment group of 14,134 people) or a placebo (a control group of 14,073 people)

  • 11 vaccine recipients got COVID; 185 of placebo recipients got COVID

Issues with RCT

  • Internal validity is the ability of an experiment to establish cause-and-effect of the treatment within the sample studied.
  • Examples of threats to internal validity:
    • Failure to randomize.
    • Failure to follow the treatment protocol/attrition.
    • Small sample sizes

Issues with RCT

  • External validity is the ability of an experimental result to generalize to a larger context or population.
  • Examples of threats to external validity:
    • Non representative samples.
    • Non representative protocol/policy.

Blocking

  • Randomization works on average but we only get one opportunity at creating treatment and control groups, and there might be imbalances in nuisance variables that could affect the outcome.

  • For example, what will happen if the treatment group for the Moderna trial happens to get younger people in it than the control group?

  • We can solve this by blocking or stratifying: randomly assigning to treatment/control within groups.

Blocking

  • Unbalanced sample - Males and Females

Blocking

  • Blocking or stratification sample

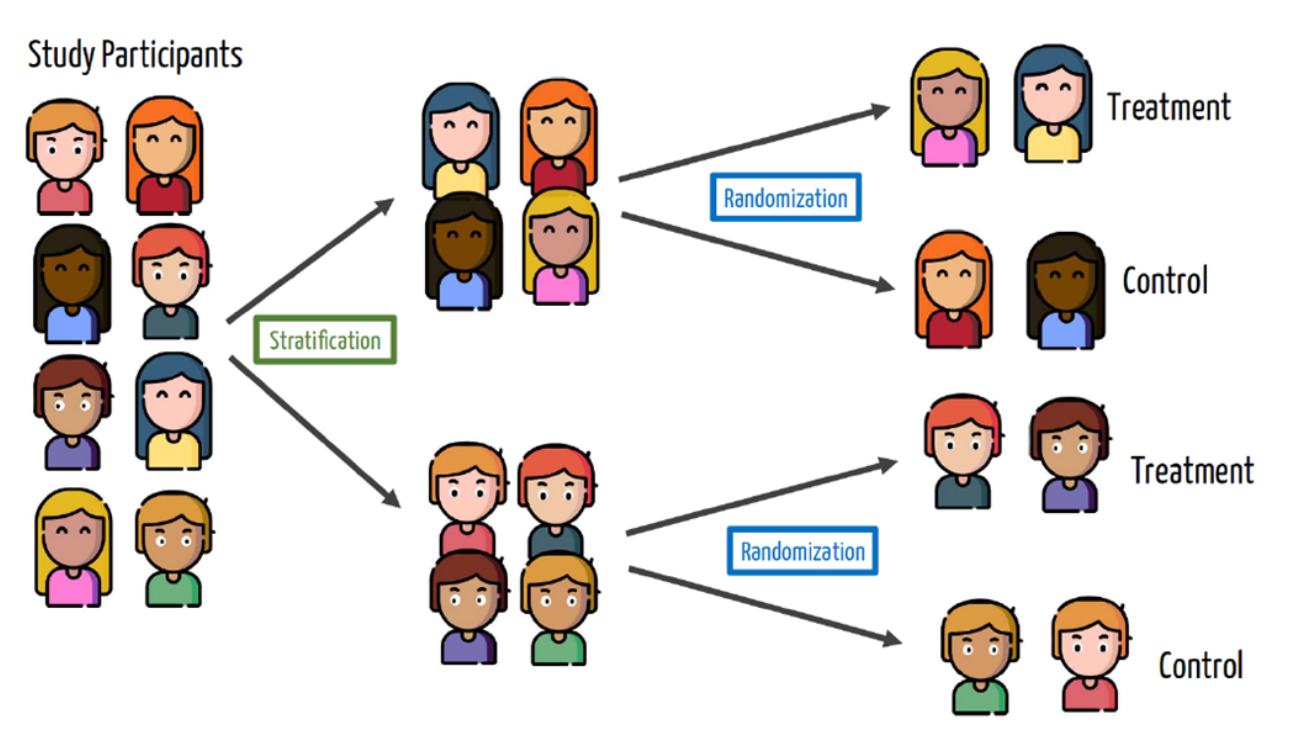
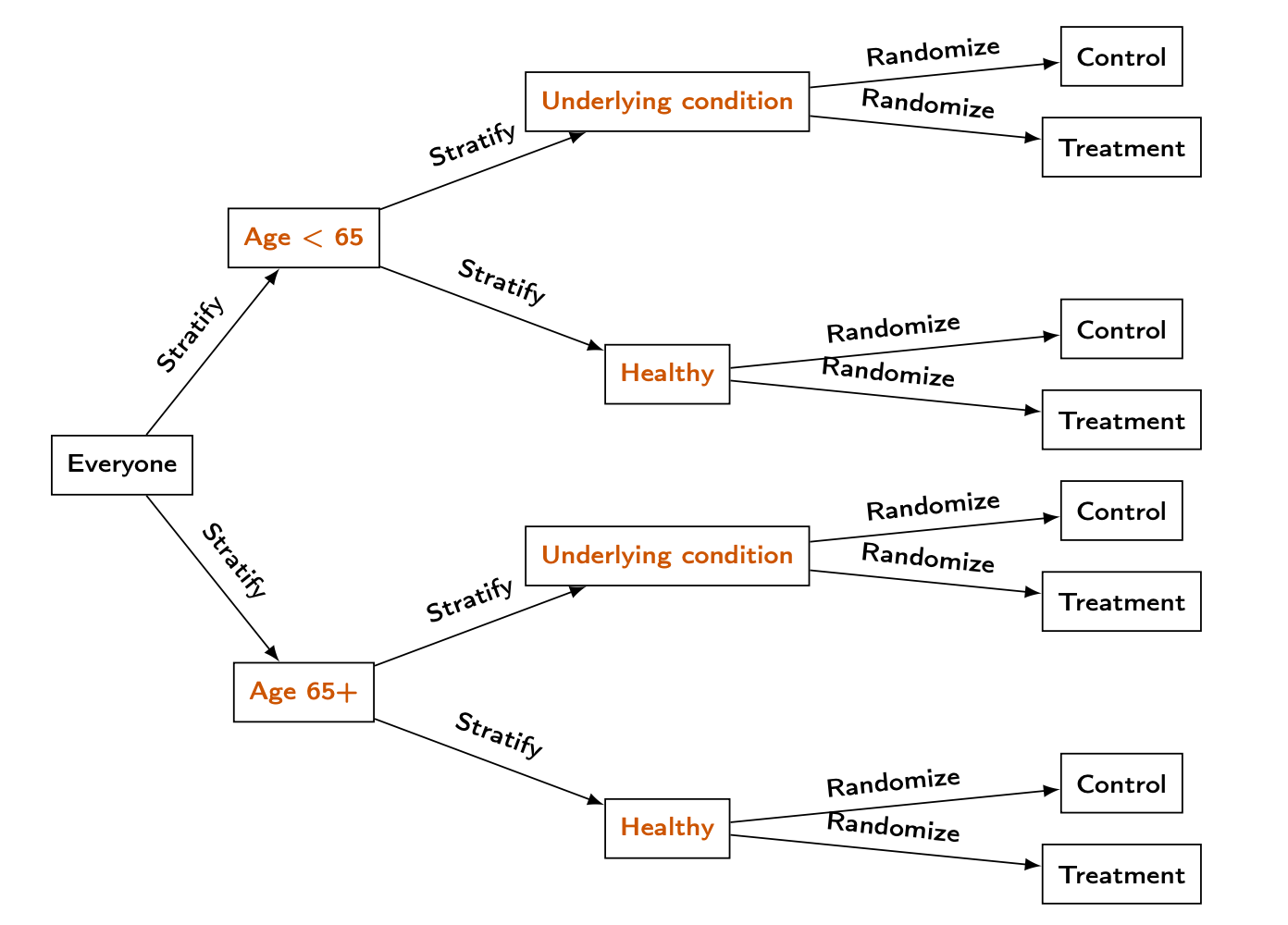
Blocking in vaccine trial

  • In the Moderna vaccine trial, they identified two possible variables that could impact COVID outcomes:

  • Age (65+ vs under 65)

  • Underlying health condition

Blocking in vaccine trial

Experiments using regression

  • Non-blocked design: use a simple regression \[ \widehat{Y} = \widehat{\beta}_0 + \widehat{\beta}_1 T, \]

  • where \(T\) is a dummy variable that is \[ T = \begin{cases} 1, & \text{for the treatment group}, \\ 0, & \text{for the control group} \end{cases} \]

  • \(\widehat{\beta}_1\) represents the estimated average treatment effect. The regression needs to be logistic if \(Y\) is categorical!

Experiments using regression

  • Blocked design: use a regression that controls for the blocking variable \(B\):

\[ \widehat{Y} = \widehat{\beta}_0 + \widehat{\beta}_1 T + \widehat{\beta}_2 B, \] where \(B\) is the fixed effect of each strata, that are interactions between categories.

  • Important: the regression needs to be logistic if \(Y\) is categorical.

Get Out The Vote (GOTV)

  • In 2002, researchers at Temple and Yale conducted a large phone banking experiment to see calling voters helps:

  • From among about 381,062 phone numbers of voters in Iowa and Michigan they randomly contacted about 12000 voters

  • The outcome Y of interest is whether each voter actually voted.

No blocking

Estimating the average treatment effect with logistic regression:

glm = glm(vote02 ~ treatment,data = GOTV, family = "binomial")
summary(glm)

Call:
glm(formula = vote02 ~ treatment, family = "binomial", data = GOTV)

Coefficients:
                   Estimate Std. Error z value            Pr(>|z|)    
(Intercept)        0.184717   0.003306  55.870 <0.0000000000000002 ***
treatmenttreatment 0.170824   0.018843   9.066 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 524839  on 381061  degrees of freedom
Residual deviance: 524756  on 381060  degrees of freedom
AIC: 524760

Number of Fisher Scoring iterations: 3
  • The coefficients are in log odds.

No blocking

  • The average treatment effect will be of approximately 19%
(exp(0.17)-1)*100
[1] 18.53049
confint(glm)
                       2.5 %    97.5 %
(Intercept)        0.1782378 0.1911978
treatmenttreatment 0.1339278 0.2077954

  • Receiving a phone call increases the likelihood of voting by 19% compared to those who did not receive a call.

  • Confidence interval for the treatment

confint(glm)
                       2.5 %    97.5 %
(Intercept)        0.1782378 0.1911978
treatmenttreatment 0.1339278 0.2077954

Blocking

  • The researchers actually used a blocking design with two variables that they thought could impact voting rates (separately from the phone calls):

  • The state of the voter (Iowa or Michigan)

  • Whether the voter was in a “competitive” district (one where there was likely to be a close election)

Blocking

Blocking

GOTV = GOTV %>%
       mutate(block = interaction(state, competiv))
glm_vote = glm(vote02 ~ treatment + block, data = GOTV, family = 'binomial')
summary(glm_vote)

Call:
glm(formula = vote02 ~ treatment + block, family = "binomial", 
    data = GOTV)

Coefficients:
                   Estimate Std. Error z value            Pr(>|z|)    
(Intercept)        0.043236   0.004146   10.43 <0.0000000000000002 ***
treatmenttreatment 0.028542   0.019279    1.48               0.139    
block1.1           0.351686   0.015168   23.19 <0.0000000000000002 ***
block0.2           0.196691   0.008866   22.18 <0.0000000000000002 ***
block1.2           0.603739   0.009515   63.45 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 524839  on 381061  degrees of freedom
Residual deviance: 520331  on 381057  degrees of freedom
AIC: 520341

Number of Fisher Scoring iterations: 4

Blocking

  • The effect of the treatment is not significant.

  • What if some callers didn’t stick to the script?

  • Many people didn’t answer the phone!

  • What about voters outside of the Midwest?

The limitations of RCTs

  • Although powerful for inferring causation, RCTs are difficult to apply.

  • They can be incredibly expensive.

  • Compliance with the treatment protocol isn’t perfect (e.g., mask-wearing, picking up the phone)

  • It can be hard to generalize beyond the participants involved in the study.

  • They can be impractical or (e.g., effect of education on performance) or unethical to conduct (e.g., seatbelts, parachutes, even medical trials)