Error, Uncertainty and the Linear Model

Measuring prediction error

Data description:

Subset of single family home sales in 3 Austin zipcodes
Variables include location, size, number of bedrooms, number of bathrooms, and many more
Focus on relationship between price, number of bedrooms, and living area (square feet) as a first example

Predicting price from area

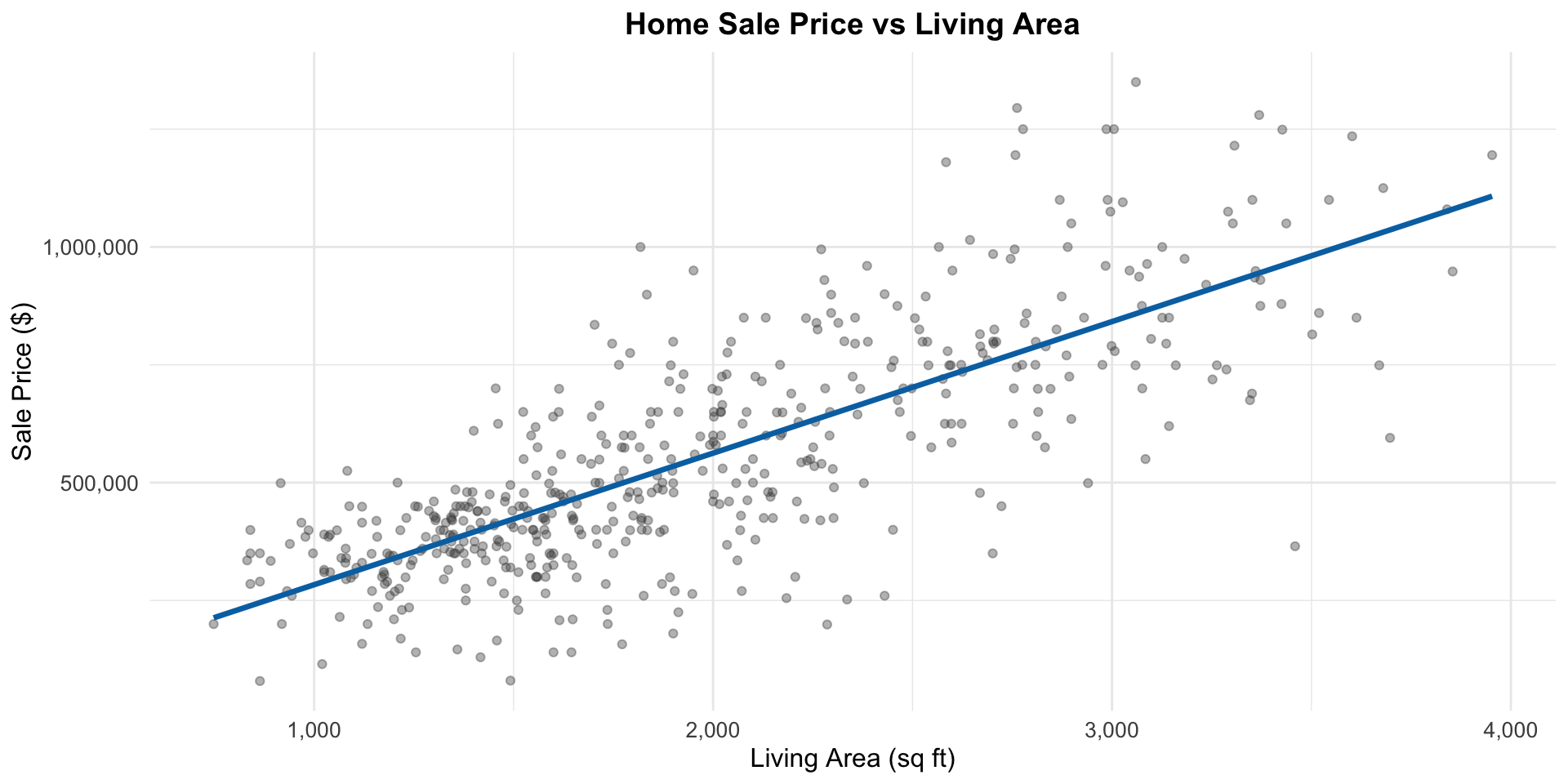
Residuals and fitted values

The fitted value (“y hat”) for observation $i$ is the predicted value from the regression line: \[ \widehat{y}_i = \widehat{\beta_0} + \widehat{\beta_1} \times \text{area}_i \]
The residual is the corresponding prediction error: \[e_i = y_i - \widehat{y}_i = \text{observed price} - \text{predicted price}\]
When a linear model fits well,
- The fitted line tells us about the part of price predictable from area
- The residuals tell us about the part of price not predictable from area

Visualizing residuals and fitted values

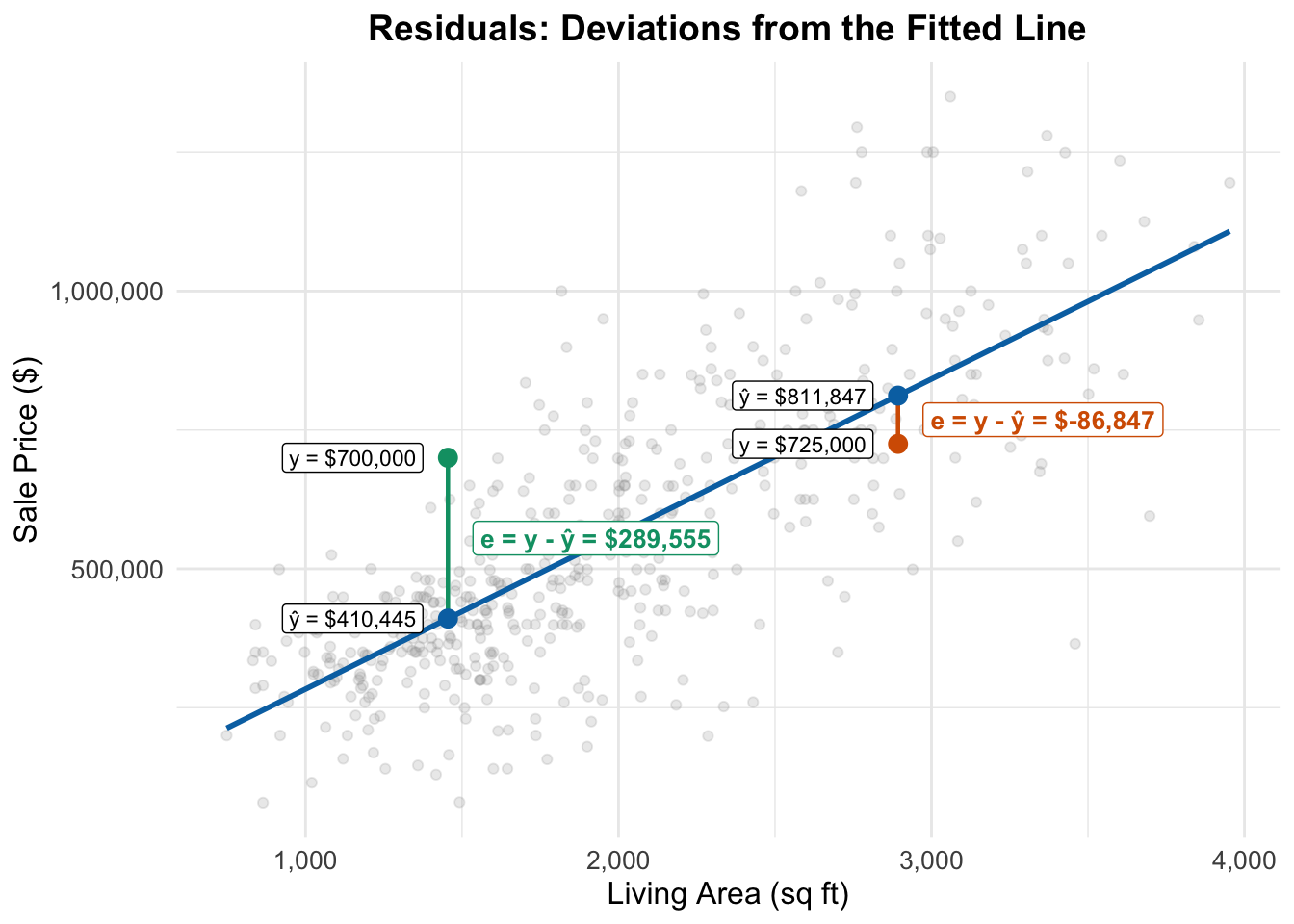
What does a residual tell us?

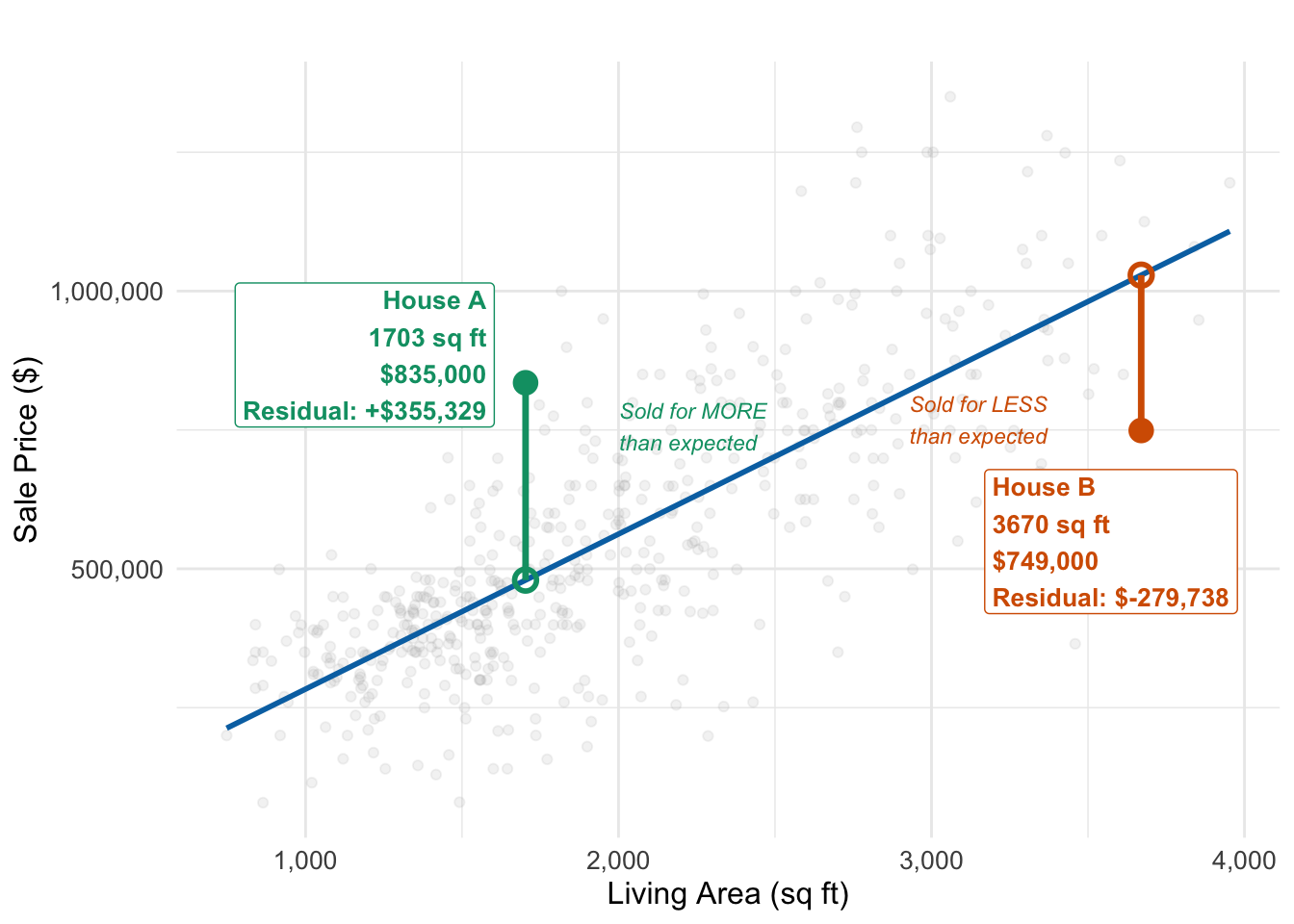
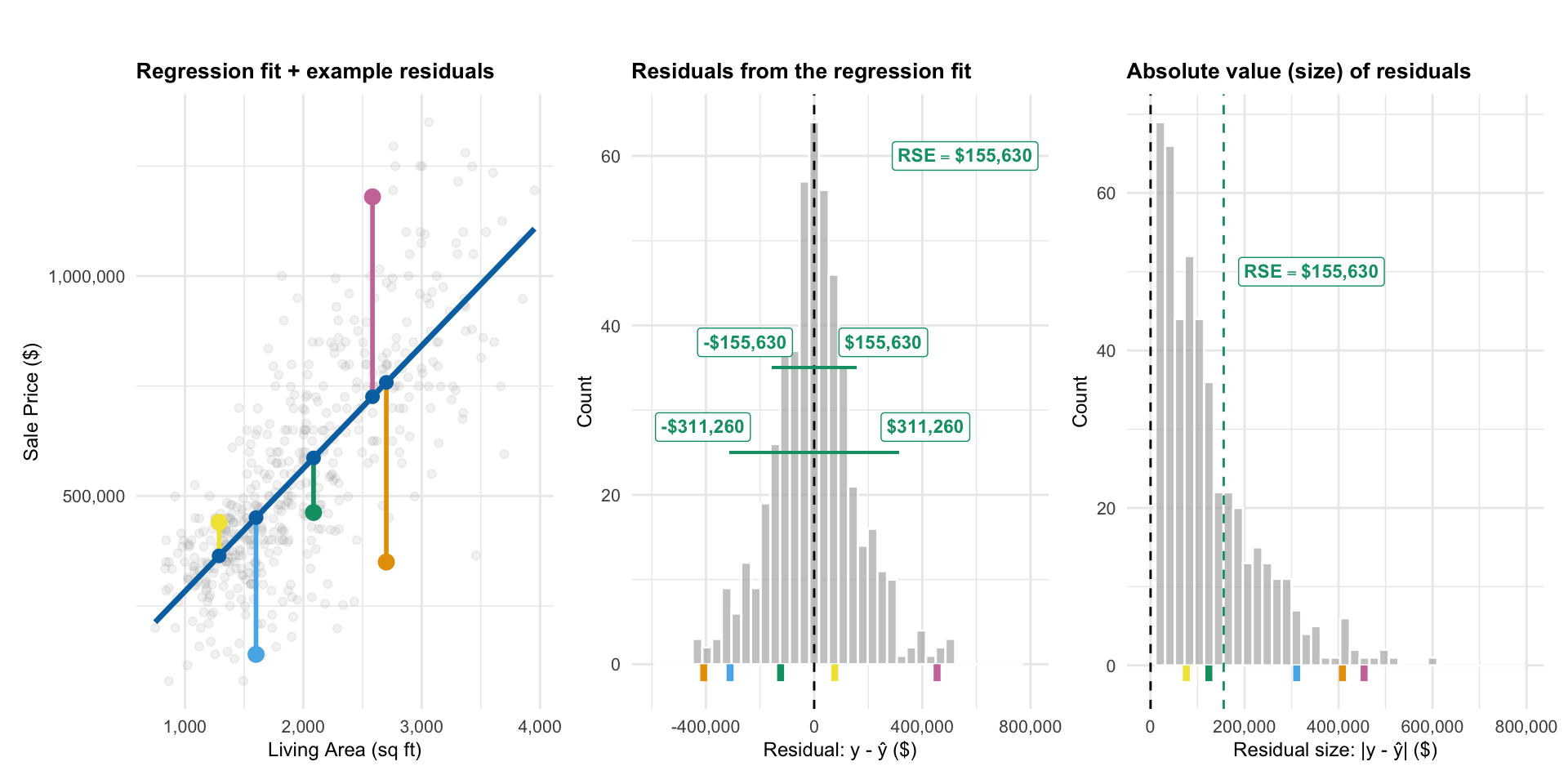
What is a “typical” residual?

The residual tells us the prediction error for a given point
The standard deviation of the residuals tells us the typical size of these prediction errors (in absolute value)
It’s a measure of how variable our prediction errors are
- Low variability: our predictions are usually close to actual values
- High variability: our predictions are often far off from actual values
In R, this is called the Residual Standard Error (RSE)

summary(fit)


Call:
lm(formula = price ~ area, data = houses)

Residuals:
    Min      1Q  Median      3Q     Max 
-604840  -90641    2955   83298  519720 

Coefficients:
             Estimate Std. Error t value            Pr(>|t|)    
(Intercept)  4296.668  21017.955  0.2044              0.8381    
area          279.139     10.101 27.6337 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 155630 on 506 degrees of freedom
Multiple R-squared:  0.60146,   Adjusted R-squared:  0.60067 
F-statistic: 763.62 on 1 and 506 DF,  p-value: < 0.000000000000000222

From line 16: RSE = $155,630

$R^2$ (R-squared)

$R^2$ is a measure of the strength of the linear relationship between the $Y$ and all $X$’s in the linear regression

$R^2$ ranges from 0 to 1
- 0 = no linear realtaionship
- 1 = perfect linear relationship
Related to correlation

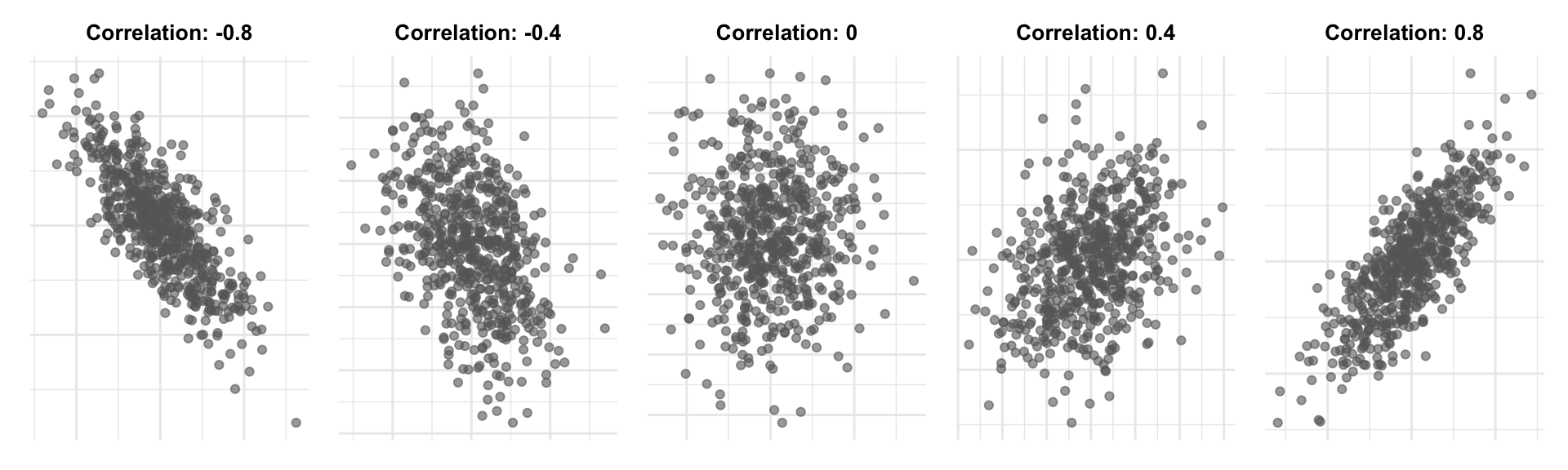
$Cor(X,Y)$ measures linear association between two variables

Between -1 and 1
Sign indicates direction of linear relationship
Magnitude indicates strength of linear relationship (0=none, $\pm 1$=perfect)

Correlation

Defining $R^2$ (R-squared)

$R^2$ has two equivalent definitions:

The squared correlation between observed and fitted values from the regression model
The proportion of variance in the outcome $Y$ “explained” by the regression model

Finding $R^2$

summary(fit)


Call:
lm(formula = price ~ area, data = houses)

Residuals:
    Min      1Q  Median      3Q     Max 
-604840  -90641    2955   83298  519720 

Coefficients:
             Estimate Std. Error t value            Pr(>|t|)    
(Intercept)  4296.668  21017.955  0.2044              0.8381    
area          279.139     10.101 27.6337 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 155630 on 506 degrees of freedom
Multiple R-squared:  0.60146,   Adjusted R-squared:  0.60067 
F-statistic: 763.62 on 1 and 506 DF,  p-value: < 0.000000000000000222

Line 17 (Multiple R-squared): $R^2 = 0.601$ (we’ll cover adjusted $R^2$ later)

$R^2 = Cor(Y, Ŷ)^2$

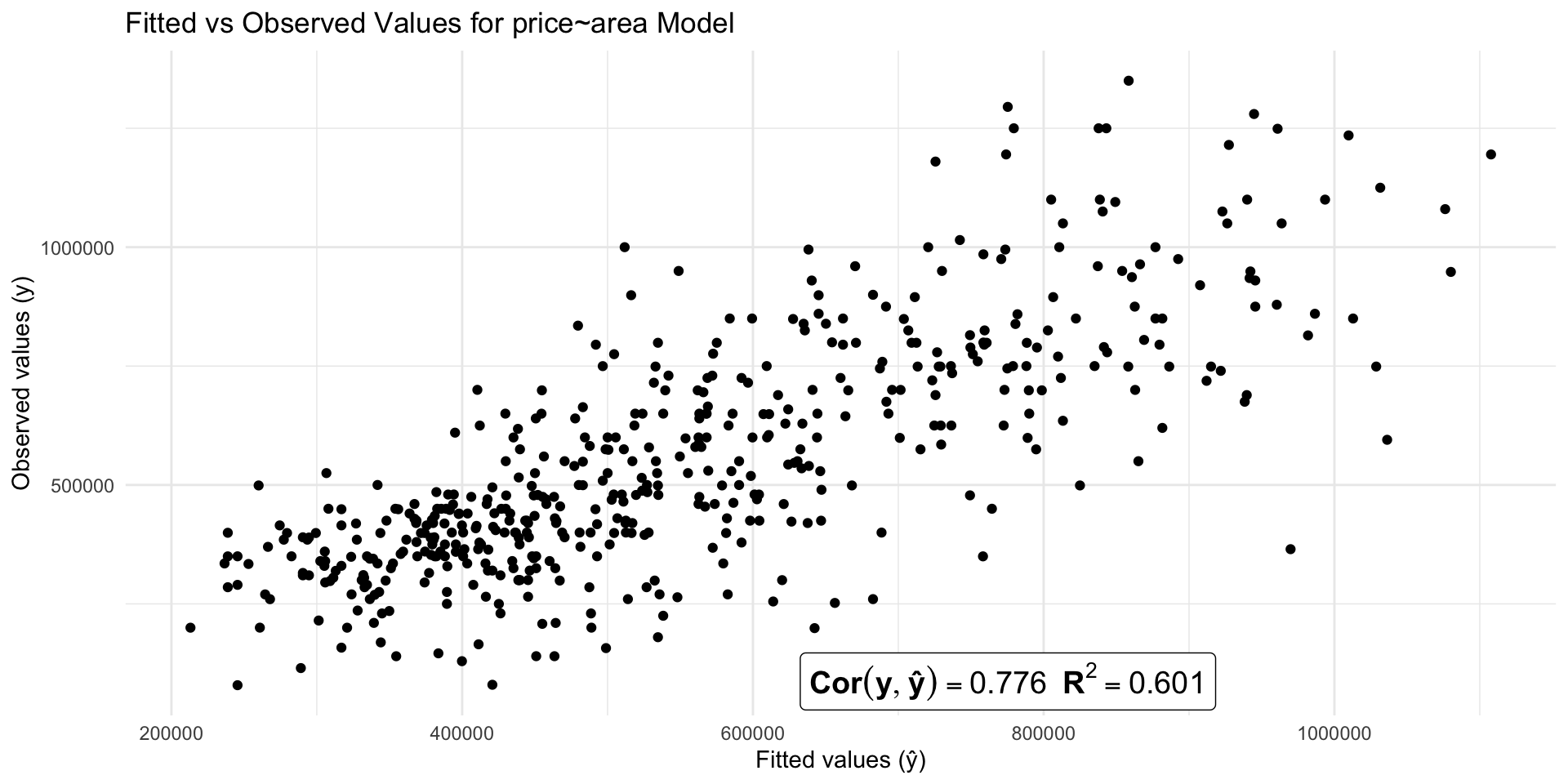
$R^2$ as generalized correlation

$R^2$ tells us how closely the predicted values track actual values
In a simple linear model, it’s the same as $Cor(X,Y)^2$
So you can think of $R^2$ as a generalization of correlation to multiple X’s

$R^2$ as generalized correlation

It inherits the same limitations as correlation:

Low $R^2$ does not imply
- No “meaningful” linear relationship
- No strong nonlinear relationship

$R^2$ as generalized correlation

High $R^2$ does not imply
- A causal relationship
- A true linear relationship
- Prediction errors are small enough to be useful
- The model will predict will for future data

$R^2$ as proportion of variance “explained”

If $R^2$ is high then our predictions track the observed values closely
$R^2$ measures how much unpredictability (variance) in the outcome “goes away” when we ues X to predict

$R^2$ as proportion of variance “explained”

\[ R^2 = \frac{\overbrace{\text{variance of Y} - \text{variance of residuals}}^{\text{variance ``explained''}}}{\text{variance of Y}} \]

Common phrasing: “$R^2$ is the proportion of variance in $Y$ explained by the model”

$R^2$ as proportion of variance “explained”

The variance of $Y$ is also the variance of the residuals under a simple regression model where we force $\hat\beta_1=0$
So we can think about $R^2$ as the reduction in variance (average size) of our residuals when using X to predict Y compared to not using X at all
If we force $\hat\beta_1=0$, all of our predictions will be $\bar y$ (the average $Y$ value)

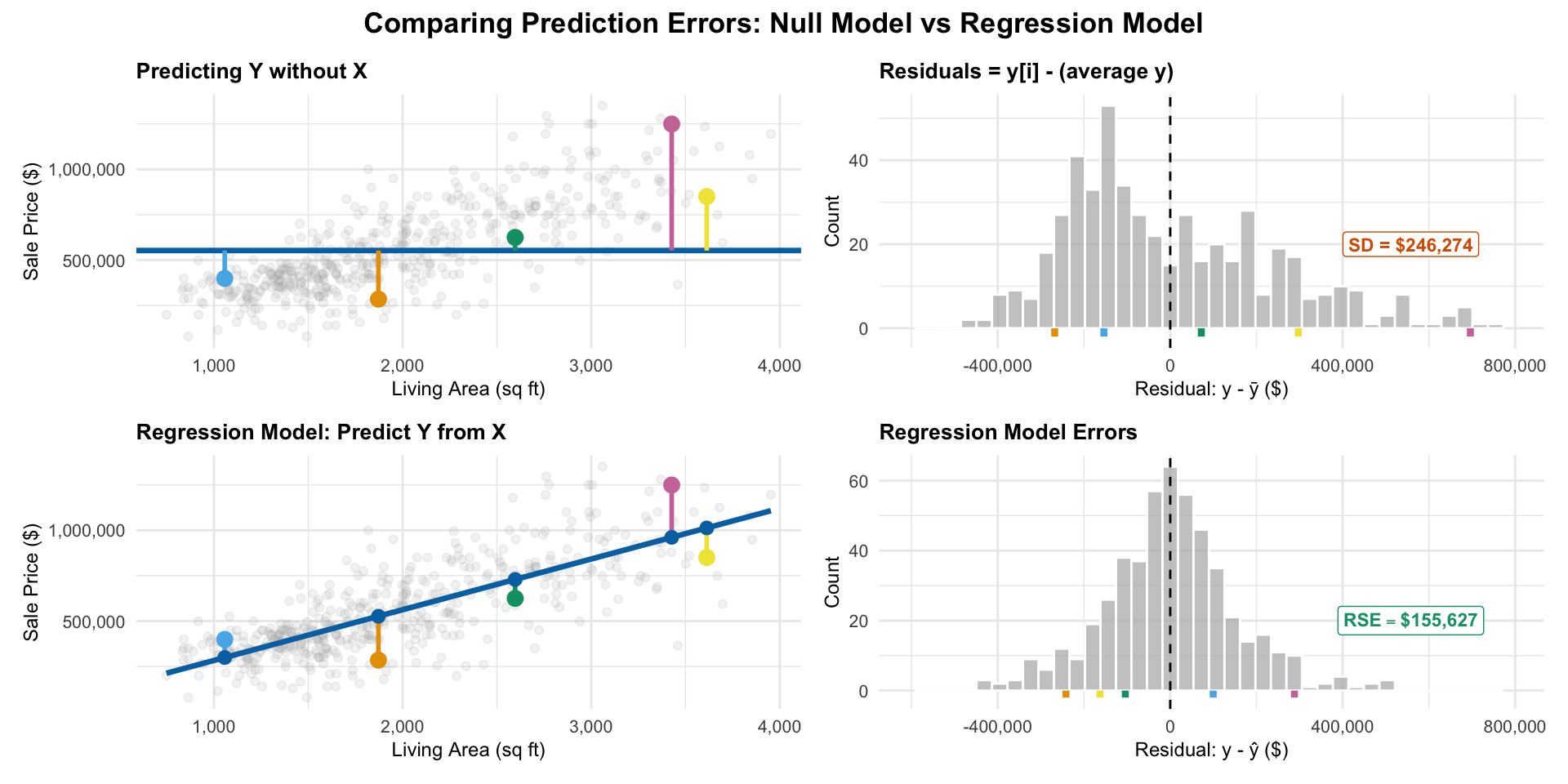
$R^2$ as proportion of variance “explained”

\[ R^2 = \frac{246,274^2 - 155,630^2}{246,274^2}\approx 0.601 \]

We say $X$ “explained” 60.1% ($R^2=0.601$) of the total variability in $Y$
Remember: this is just a way of quantifying how closely the line tracks actual values
- You can predict something without being able to explain why it happens!

Multiple or Adjusted $R^2$?

The only difference is how residual variance is estimated
In practice, the difference is usually small
- If they’re very different then neither is very reliable
On a HW/Quiz/Exam you can use either
Later we’ll see how to get more accurate measures of prediction error

$R^2$ or RSE?

$R^2$ measures the strength of the linear relationship between Y and the X’s
- Since it’s a relative measure, we don’t know how big our prediction errors are likely to be
$RSE$ measures the typical size of our prediction errors using X to predict Y
- Since it’s an absolute measure, we don’t know how strong the linear relationship is

Both can be useful, but in practice RSE is usually more relevant.

$R^2$ or RSE?

Predicting the price of a house from its area:

R^2 = 0.601
RSE = $155,630

Pretty strong linear relationship, but typical prediction errors are still very large!

$R^2$ doesn’t add up

We can use $R^2$ to measure “independent” contributions of multiple $X$ variables
Compare $R^2$ from models with different sets of $X$ variables
- Area: $R^2$ = 0.601
- Beds: $R^2$ = 0.137
- Area and Beds $R^2$ = 0.615 $\neq 0.601+0.137$
Adding beds once you know area -> only about 1.4% more variance explained

Why?

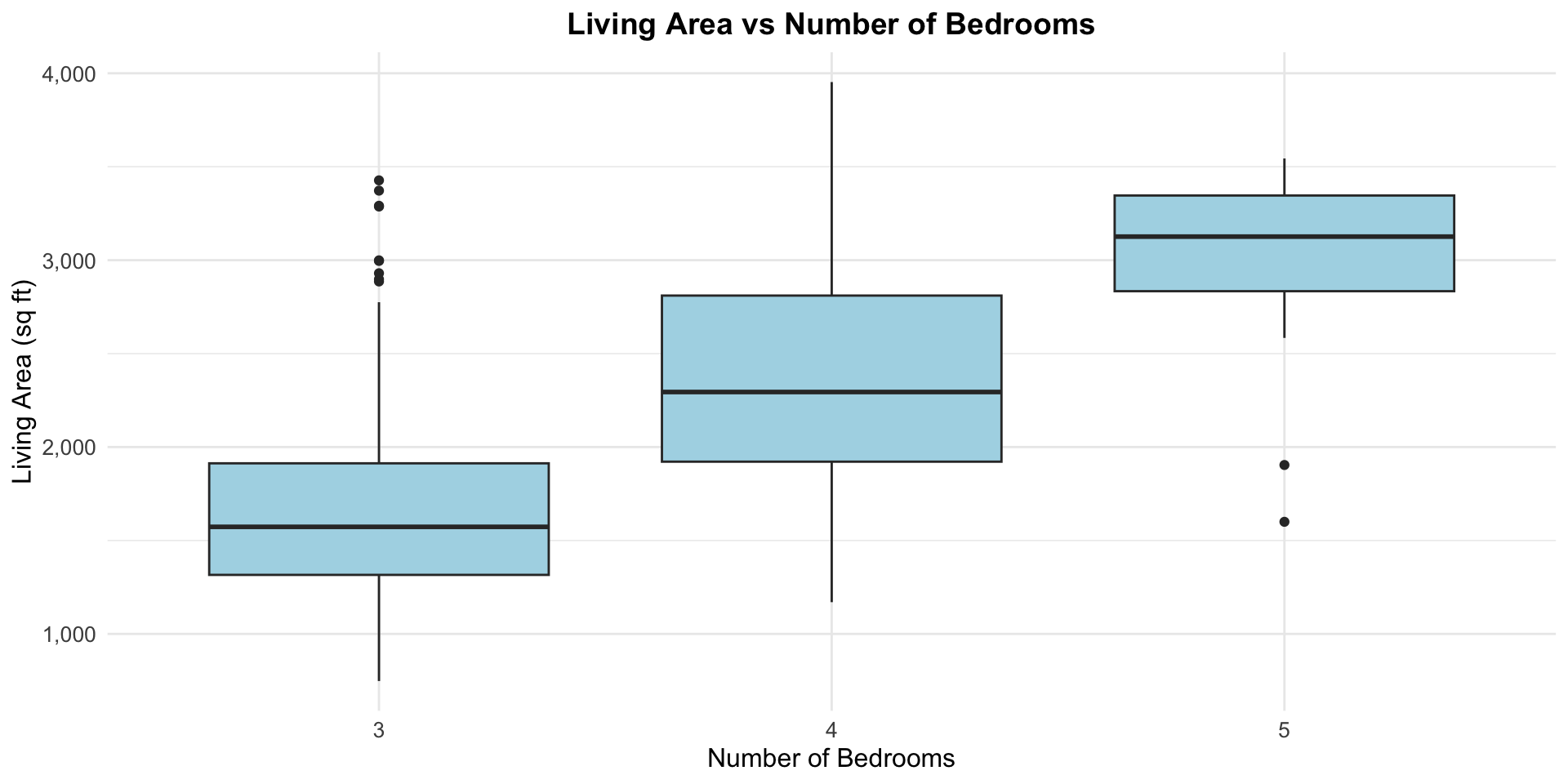
Area already contains a lot of information about beds
The new information we get from introducing beds is not that useful for predicting prices
Compare this to starting with beds and adding area – we get a big boost in $R^2$

Prediction isn’t everything

Notice that the area and area+beds model have very similar $R^2$ values
The RSE values are also similar
- Area only: 155627
- Area + Beds: 153047
Both models predict prices about equally well (or badly)
- But they tell very different stories about what an additional sqft is worth!

Incorporating uncertainty

Accounting for error and uncertainty

So far we’ve focused on estimated coefficients and predictions
We know our predictions will be wrong – how wrong are the likely to be?
We know our coefficients don’t match the true population values – how close are they?

The simple linear regression model

We need a model for our data to answer these questions. Our model has four components:

Linearity
Independence of prediction errors
Normality of prediction errors
Equal variance of prediction errors

Linearity

The relationship between $Y$ and each $X$ is linear:

$Y = \beta_0 + \beta_1 X_{1} + \beta_2 X_{2} + ... + \beta_p X_{p} + \epsilon$

$\beta_0, \beta_1, ..., \beta_p$ are the true/population regression coefficients
$\epsilon$ is the true error if we predict $Y$ using the true regression coefficients

Our other assumptions are about those true error terms $\epsilon$…

Independence

Each observation has an independent true error term
If my neighbor’s house sells for more than expected, that doesn’t tell me anything about whether my house will sell for more or less than expected
If the last house sells for less than expected, that doesn’t tell us anything about whether the next house will sell for more or less than expected

Normality

The true error terms $\epsilon$ are normally distributed and centered at zero

The average error over many predictions is zero
Over-prediction and under-prediction are equally likely
Most errors are small, but large errors are possible

Equal Variance

The true error terms $\epsilon$ all have the same standard deviation $\sigma$
The size of the true errors does not depend on the values of the X’s (or anything else)
- For example, errors are about the same size (on average) for small and large houses

The linear model

Putting the LINE assumptions together, we have the full linear regression model:

\[ Y = \beta_0 + \beta_1 X_{1} + \beta_2 X_{2} + ... + \beta_p X_{p} + \epsilon \]

\[ \epsilon\sim N(0, \sigma^2)\text{ independently for each observation} \]

For an individual observation with predictors $X$, we have:

\[ (Y\mid X) \sim N(\beta_0 + \beta_1 X_{1} + \beta_2 X_{2} + ... + \beta_p X_{p}, \sigma^2) \]

Visualizing the linear model

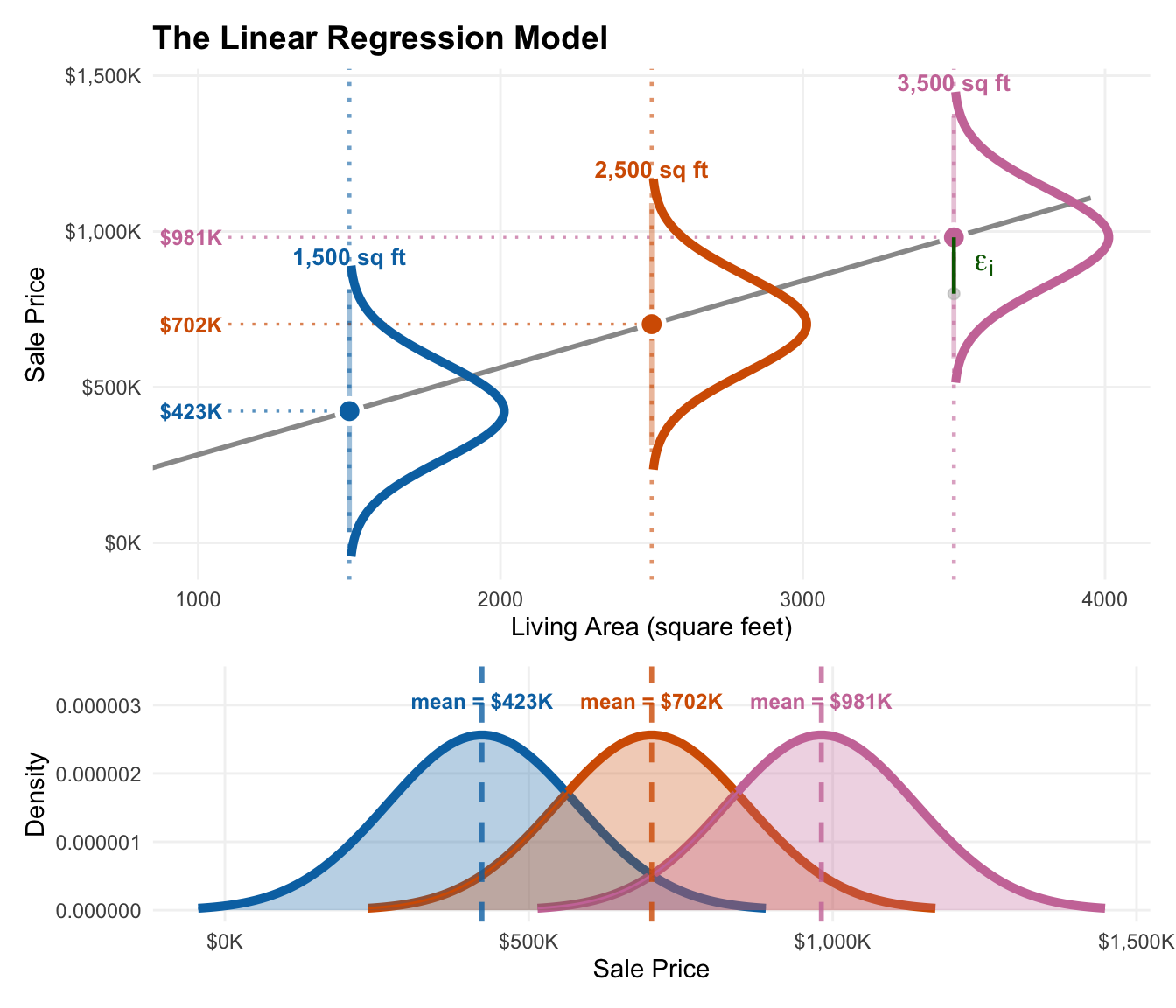
Estimates vs True Values

Our $\hat \beta_0, \hat \beta_1, ..., \hat \beta_p$ are just estimates of the true $\beta_0, \beta_1, ..., \beta_p$
The residuals estimate the true prediction errors
The RSE (standard deviation of residuals) is an estimate of the true $\sigma$ (error standard deviation)

Accounting for uncertainty in estimates

If we want to know how uncertain our estimates are, we need to quantify their variability.
We can do this using the sampling distribution of our estimates (how much they change over repeated samples)
More specifically, we can compute confidence intervals

Confidence intervals

A confidence interval gives a range of plausible values for a population parameter (e.g., a regression coefficient)
These are possible values of the true coefficients that are consistent with our observed data at a given level of confidence (e.g., 95%)
If our LINE assumptions hold, these are easy to get:

confint(fit)

                   2.5 %      97.5 %
(Intercept) -36996.53678 45589.87298
area           259.29353   298.98532

Returning to course evaluations


Call:
lm(formula = eval ~ beauty, data = profs)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.8002 -0.3630  0.0725  0.4021  1.1037 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept)   3.9983     0.0253  157.73 < 0.0000000000000002 ***
beauty        0.1330     0.0322    4.13             0.000042 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.545 on 461 degrees of freedom
Multiple R-squared:  0.0357,    Adjusted R-squared:  0.0336 
F-statistic: 17.1 on 1 and 461 DF,  p-value: 0.0000425

Is there evidence for a linear relationship?

confint(model_simple)

             2.5 % 97.5 %
(Intercept) 3.9485  4.048
beauty      0.0698  0.196

The range of plausible values for the slope $\beta_1$ is (0.07, 0.20)
No linear relationship would mean $\beta_1=0$
All the plausible values are positive, so we have statistically significant evidence of a positive linear relationship between beauty and evaluations

How strong is the linear relationship?

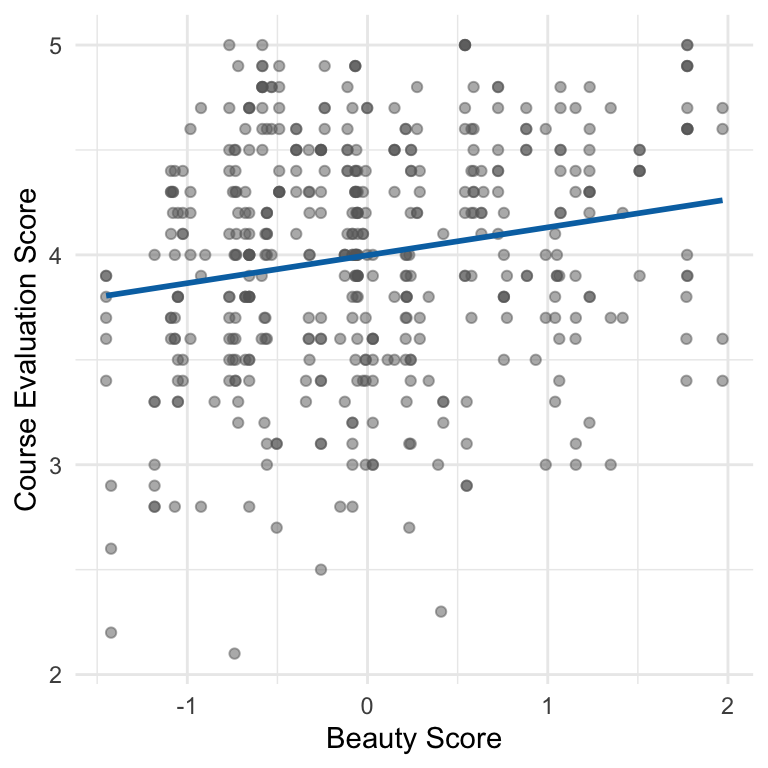
$\text{Cor}(\text{beauty, eval}) = 0.19$
$R^2$ = 0.036 – only 3.6% of the variance in eval is explained by beauty
But we have strong statistical evidence that this (weak) linear relationship holds among the population of all instructors
- i.e., it isn’t just a fluke in this particular sample

How strong is the linear relationship?

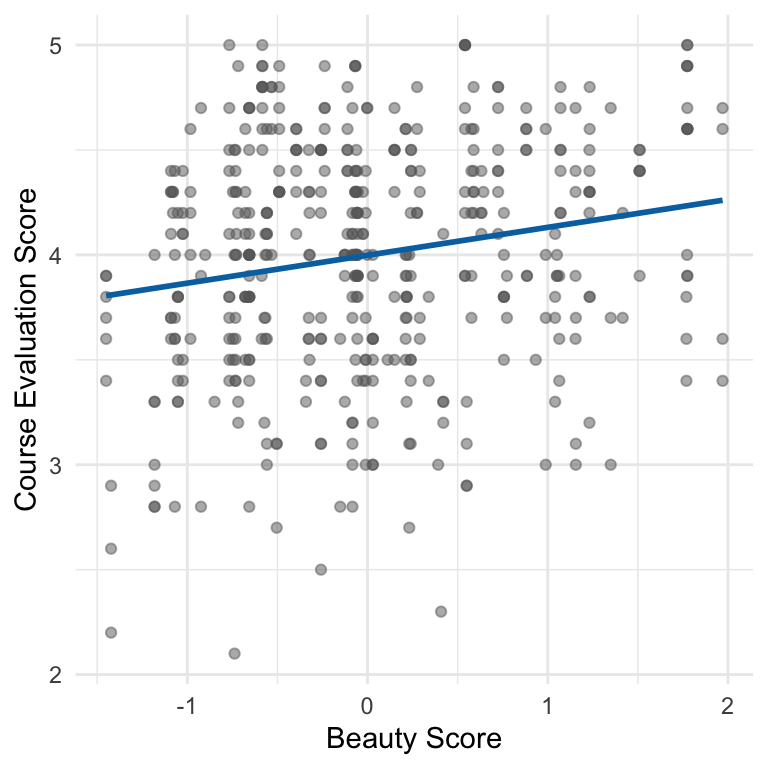
Remember: $R^2$ doesn’t tell us directly how confident we are that a linear relationship exists
In this case we have strong evidence of a weak linear relationship
This is because many factors unrelated to beauty affect eval scores

Accounting for uncertainty in predictions

If I’m selling a house I’d like to know:

What’s the most likely sale price (best prediction)?
What’s a range of likely sale prices (prediction interval)?

Prediciton intervals

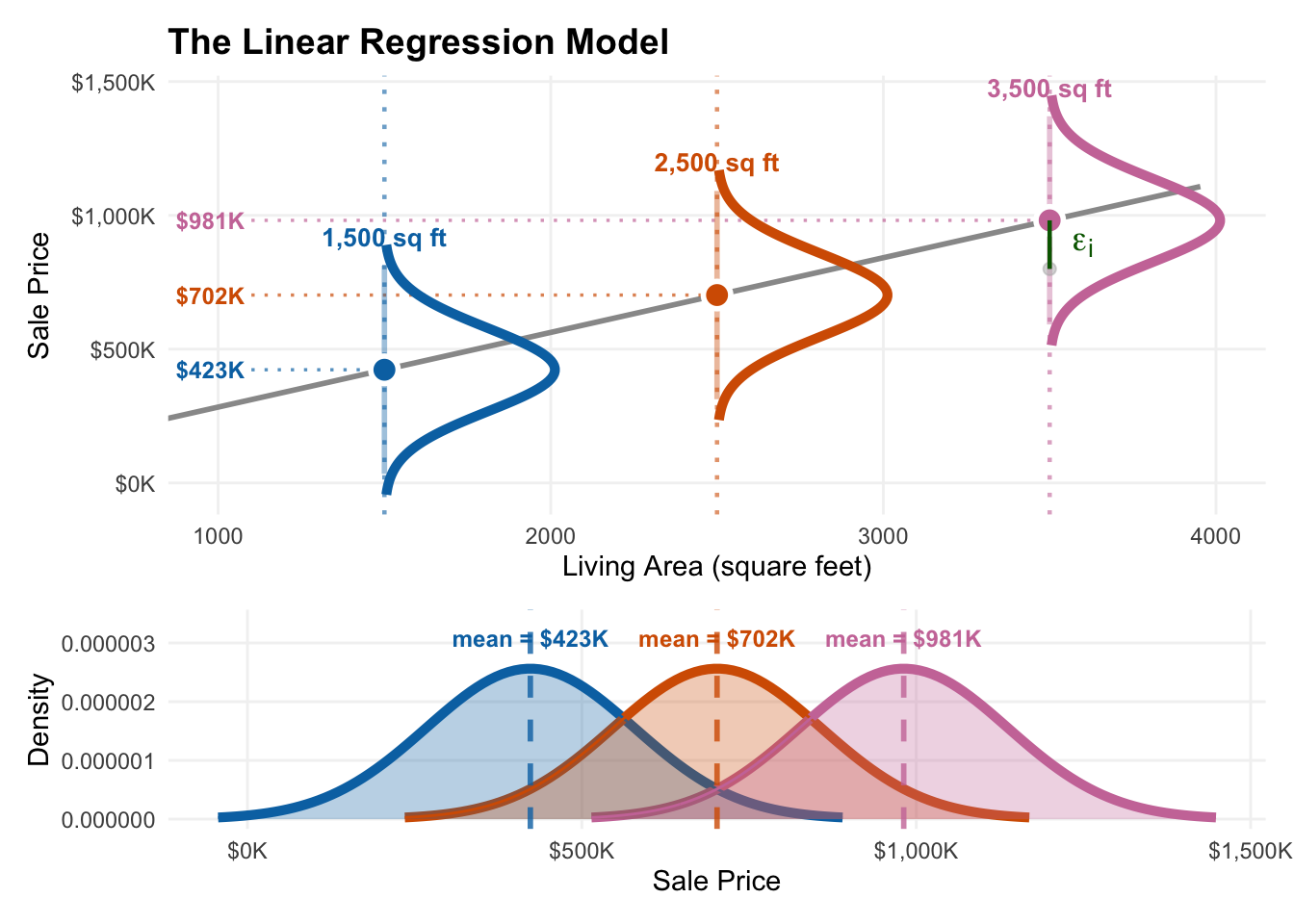
Our model: Actual prices for houses of a given size will:

Have normal distributions
Centered at the predicted value (location on the line)
With standard deviation $\sigma$

95% of the time, actual prices fall within $\pm 2\sigma$ of the predicted price (if we knew the true line and $\sigma$)

Prediction intervals

Under our LINE assumptions, we can get prediction intervals for new observations that account for both:

Uncertainty in our estimated regression line
The inherent variability in actual outcomes around that line

new_house = data.frame(area = 2000)
predict(fit, newdata = new_house, 
  interval = "prediction")

     fit    lwr    upr
1 562576 256519 868632

95% prediction interval: ($256,518, $868,632)

Prediction intervals

new_house = data.frame(area = 2000)
predict(fit, newdata = new_house, 
  interval = "prediction")

     fit    lwr    upr
1 562576 256519 868632

There’s a 95% chance that a new house will sell for a price in this range
95% of all future houses with 2000 sq ft will sell for between $256,518 and $868,632

Error, Uncertainty and the Linear Model

Measuring prediction error

Data description:

Predicting price from area

Residuals and fitted values

Visualizing residuals and fitted values

What does a residual tell us?

What is a “typical” residual?

\(R^2\) (R-squared)

Correlation

Defining \(R^2\) (R-squared)

Finding \(R^2\)

\(R^2 = Cor(Y, Ŷ)^2\)

\(R^2\) as generalized correlation

\(R^2\) as generalized correlation

\(R^2\) as generalized correlation

\(R^2\) as proportion of variance “explained”

\(R^2\) as proportion of variance “explained”

\(R^2\) as proportion of variance “explained”

\(R^2\) as proportion of variance “explained”

Multiple or Adjusted \(R^2\)?

\(R^2\) or RSE?

\(R^2\) or RSE?

\(R^2\) doesn’t add up

Why?

Prediction isn’t everything

Incorporating uncertainty

Accounting for error and uncertainty

The simple linear regression model

Linearity

Independence

Normality

Equal Variance

The linear model

Visualizing the linear model

Estimates vs True Values

Accounting for uncertainty in estimates

Confidence intervals

Returning to course evaluations

Is there evidence for a linear relationship?

How strong is the linear relationship?

How strong is the linear relationship?

Accounting for uncertainty in predictions

Prediciton intervals

Prediction intervals

Prediction intervals